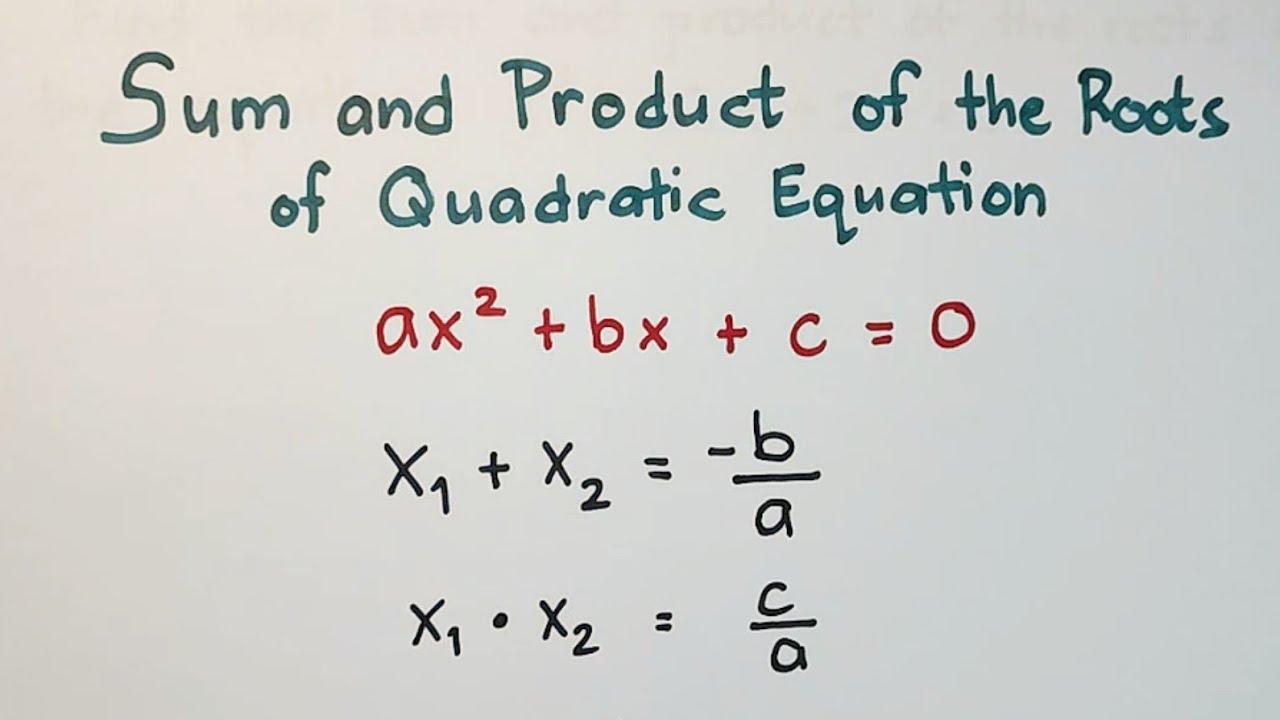Product Of Sums Equals Sum Of Products . When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let us prove of for two sums. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. Let’s investigate the cosine identity first. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. In general, one can write a product of sums as a sum of a products: Let’s investigate the cosine identity first.
from www.youtube.com
(∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. Let’s investigate the cosine identity first. Let us prove of for two sums. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. In general, one can write a product of sums as a sum of a products:
Sum and Product of the Roots of Quadratic Equation Finding the
Product Of Sums Equals Sum Of Products (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. Let’s investigate the cosine identity first. Let us prove of for two sums. Let’s investigate the cosine identity first. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. In general, one can write a product of sums as a sum of a products:
From www.youtube.com
5. Convert each of the following expressions into sum of products and Product Of Sums Equals Sum Of Products Let’s investigate the cosine identity first. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. In general, one can write a product of sums as a sum of a products: Let’s investigate. Product Of Sums Equals Sum Of Products.
From www.coursehero.com
[Solved] Obtain the simplified expression in sum of products for the Product Of Sums Equals Sum Of Products Let’s investigate the cosine identity first. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. In general, one can write a product of sums as a sum of a products: Let us. Product Of Sums Equals Sum Of Products.
From www.youtube.com
Sum of Products (SOP) and Product of Sum (POS) Canonical Standard Product Of Sums Equals Sum Of Products Let us prove of for two sums. Let’s investigate the cosine identity first. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. In general, one can write a product of sums as a sum of a products: (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj.. Product Of Sums Equals Sum Of Products.
From nanohub.org
Resources ECE 595Z Lecture 4 Advanced Boolean Algerbra Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let us prove of for two sums. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. In. Product Of Sums Equals Sum Of Products.
From www.slideserve.com
PPT Chapter 4 Combinational Logic Circuits PowerPoint Presentation Product Of Sums Equals Sum Of Products In general, one can write a product of sums as a sum of a products: Let’s investigate the cosine identity first. Let us prove of for two sums. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i,. Product Of Sums Equals Sum Of Products.
From www.studocu.com
Sum of Products(SOP) and Product of Sums(POS) Sum of Products(SOP Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. In general, one can write a product of sums as a sum of a products: Let us prove of for two sums. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this,. Product Of Sums Equals Sum Of Products.
From courses.cs.washington.edu
Productofsums canonical form Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. Let’s investigate. Product Of Sums Equals Sum Of Products.
From www.youtube.com
Product Of Sum (Canonical To Minimal Form)(हिन्दी ) YouTube Product Of Sums Equals Sum Of Products If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. Let’s investigate the cosine identity first. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. Let us prove of for two sums. Let’s investigate the cosine identity first. When you distribute the product over. Product Of Sums Equals Sum Of Products.
From nanohub.org
Resources ECE 595Z Lecture 4 Advanced Boolean Algerbra Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. Let us prove of for two sums. Let’s investigate the cosine identity first. In general, one can write a product of sums as a sum of a products: If the boolean expression is ab+bc.then the product of. Product Of Sums Equals Sum Of Products.
From www.youtube.com
Product of the Sum and Difference of Two Terms Grade 7 MELC YouTube Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. In general, one can write a product of sums as a sum of a products: (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. Let’s investigate the cosine identity first. Let’s investigate the cosine identity first. Let. Product Of Sums Equals Sum Of Products.
From courses.cs.washington.edu
Productofsums canonical form (cont’d) Product Of Sums Equals Sum Of Products Let’s investigate the cosine identity first. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. Let’s investigate the cosine identity first. In general, one can write a product of sums as a sum of. Product Of Sums Equals Sum Of Products.
From www.electronics-lab.com
Sum of Product Product Of Sums Equals Sum Of Products (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. Let’s investigate the cosine identity first. Let us prove of for two sums. If the boolean expression is ab+bc.then the product of. Product Of Sums Equals Sum Of Products.
From www.youtube.com
Product of Sums vs Sum of Products YouTube Product Of Sums Equals Sum Of Products If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. In general, one can write a product of sums as a sum of a products: Let’s investigate. Product Of Sums Equals Sum Of Products.
From www.coursehero.com
[Solved] . 5. Convert the following expressions to sumofproduct forms Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. Let us prove of for two sums. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈ i, j ∈ jxiyj. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this,. Product Of Sums Equals Sum Of Products.
From www.coursehero.com
[Solved] Using the truth table from Problem 1, and the sumofproducts Product Of Sums Equals Sum Of Products If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. In general, one can write a product of sums as a sum of a products: Let’s investigate. Product Of Sums Equals Sum Of Products.
From www.scribd.com
Product of sums Simplification Simplify the following Boolean function Product Of Sums Equals Sum Of Products Let’s investigate the cosine identity first. If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. In general, one can write a product of sums as a sum of a products: Let us. Product Of Sums Equals Sum Of Products.
From www.youtube.com
Representing Boolean Functions Sum of Products and Products of Sum Product Of Sums Equals Sum Of Products When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. In general, one can write a product of sums as a sum of a products: If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. (∑ i ∈ ixi)(∑ j ∈ jyj) =. Product Of Sums Equals Sum Of Products.
From worksheetmediaoohed.z5.web.core.windows.net
Sum And Product Of The Roots Calculator Product Of Sums Equals Sum Of Products If the boolean expression is ab+bc.then the product of sum expression is (a+b)(b+c).to find this, the complement of sum product. When you distribute the product over the left sum you get $$ \left( \sum_i x_i\right) \left( \sum_j. Let’s investigate the cosine identity first. Let’s investigate the cosine identity first. (∑ i ∈ ixi)(∑ j ∈ jyj) = ∑ i ∈. Product Of Sums Equals Sum Of Products.